Guess the Largest Number Paradox

Many statistical paradoxes boil down to an imprecise problem statement, but this is one paradox that is truly astonishing, where we seem to get information from absolutely nothing.

The Problem

Consider a simple game. There are two pieces of face-down paper on the table, and there is a number written on each. You don’t know anything about the numbers. You flip over one of the pieces of paper at random, and read the number on it. Now, you need to decide if you think this is the larger of the two numbers. What do you do?

Intuitively, there is no better solution that guessing randomly, and you cannot guess which number is bigger more than 50% of the time. You have no information about the other number, so you might as well guess randomly.

The Solution

However, this is not actually the best that you can do. There is a way to guess correctly strictly more than 50% of the time, formalized by Thomas Cover in 1987 in only a single paragraph.1

Pick a “splitting number” \(T\) at random according to a normal distribution. When you reveal the number \(X\), compare \(T\) and \(X\). If \(X >= T\), guess that \(X\) is the larger number. If \(X < T\), guess that \(X\) is the smaller number.

Why does it work?

This solution works because you always answer correctly when \(T\) is between the two numbers, and answer correctly 50% of the time otherwise. It’s easiest to see this visually.

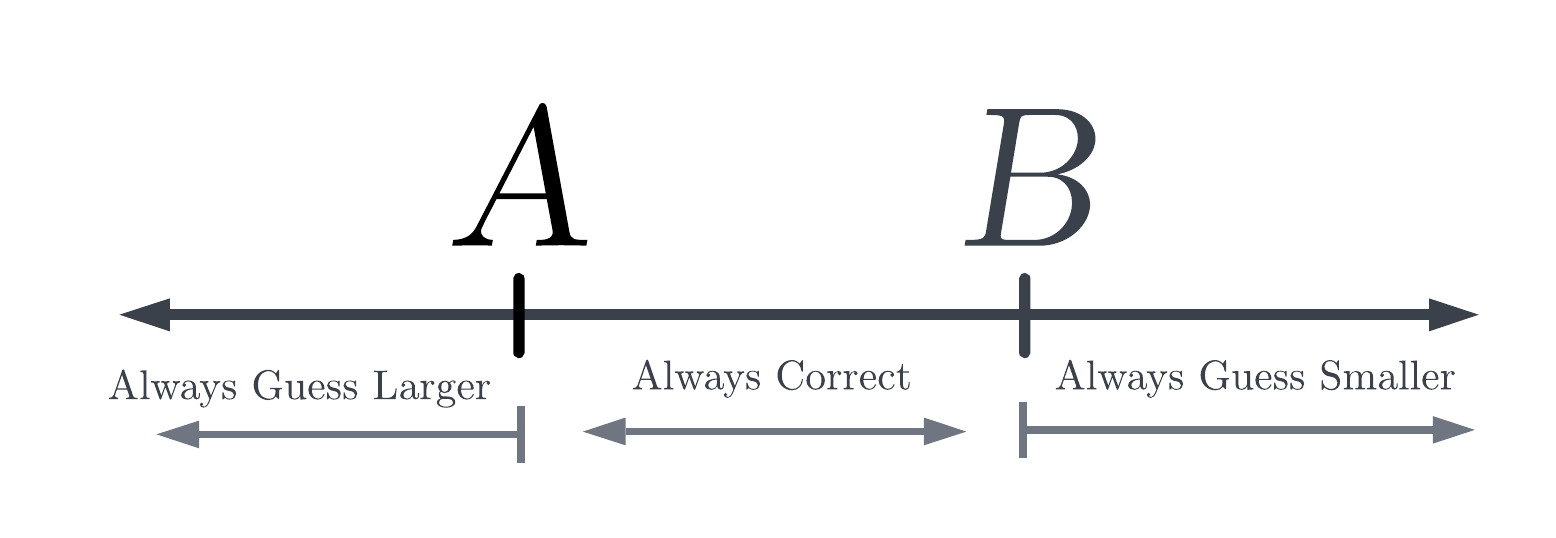
Let’s call the smaller of the two numbers \(A\), and the larger of the two numbers \(B\). Alone, that looks like this:

Now, we create our random guess \(T\). We first investigate the easy options, where \(T\) is smaller than both numbers or larger than both numbers.

In this case, we always guess that the number revealed is the larger of the two, based on our strategy from before. We will be correct if \(B\) is chosen, and wrong if \(A\) is chosen. Because we choose between \(A\) and \(B\) randomly, we will pick \(B\) 50% of the time, and thus will guess correctly 50% of the time.

In this case, we always guess that the number revealed is the smaller of the two, based on our strategy from before. We will be correct if \(A\) is chosen, and wrong if \(B\) is chosen. Similarly to before, we will pick \(A\) 50% of the time, and thus will guess correctly 50% of the time.

If \(T\) is between \(A\) and \(B\), our guess depends on which of \(A\) and \(B\) is chosen.

If \(B\) is chosen, we will correctly say that \(B\) is the larger of the two.

Similarly, If \(A\) is chosen, we will correctly say that \(A\) is the smaller of the two. If \(T\) is between \(A\) and \(B\), we always answer correctly.

We can summarize our results like the below.

Analysis

How likely is it that we guess correctly? We can summarize it into the formula below by splitting into three cases based on how \(T\) compares to \(A\) and \(B\).

\[\begin{align} P(\text{correct}) &= \frac{P(T \leq A)}{2} + P(A < T \leq B) + \frac{P(T > B)}{2} \\ &= \frac{P(T \leq A) + P(T > B)}{2} + P(A < T \leq B) \\ &= \frac{1 - P(A < T \leq B)}{2} + P(A < T \leq B) \\ &= \frac{1}{2} + \frac{P(A < T \leq B)}{2} \end{align}\]

Now, all we need to do is figure out how likely we are to have \(T\) between \(A\) and \(B\). Because we picked out \(T\) from a normal distribution, we can directly solve for this probability. With a little inspection, we can see that this probability is strictly greater than 0 for all positive numbers, and as such the odds that \(T\) is between \(A\) and \(B\) is also strictly positive.

\[P(A < T \leq B) = \int_A^B \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} dx\]

Thus, our final equation for the probability we guess correctly is

\[P(\text{correct}) = \frac{1}{2} + \int_A^B \frac{1}{\sqrt{8\pi}} e^{-\frac{x^2}{2}} dx\]

We can evaluate this for some different values of \(A\) and \(B\) to investigate how this behaves.

A: 0  B: 1
   Probability: 0.6707
A: 0  B: 10
   Probability: 0.75
A: 5  B: 10
   Probability: 0.50000014
A: 7  B: 10
   Probability: 0.500000000001

It’s clear that the probability goes down when \(A\) and \(B\) are closer to each other, and also goes down when \(A\) and \(B\) are farther from 1. In fact, by the time \(A\) and \(B\) are both greater than 10, the difference from 0.5 is below the precision of most software. However, it always positive.

This is the real caveat to the strong statement of “strictly greater than .5”. Although the probability of guessing correctly is better than one half, it is not uniformly greater than one half. Unless we assume some prior distribution of \(A\) and \(B\), this strategy is basically exactly as effective as randomly guessing.

More precisely, as long as you know nothing about \(A\) and \(B\), you cannot ever get measurably far from a probability of one half. For any \(\epsilon > 0\), you can never achieve a probability of guessing correctly that is at least \(\frac{1}{2} + \epsilon\).

Even further, if we do know something about the distribution of \(A\) and \(B\), this is still not the best strategy. If we know that \(A\) and \(B\) come independently from some distribution \(F\), we should still use a “splitting number” strategy, but our splitting point \(T\) should be exactly the median of the distribution \(F\).

This lines up with intuition about this type of problem. If you know that \(A\) and \(B\) are drawn uniformly from the range \([0, 10]\), we guess that numbers less than 5 are the smaller of the two, and numbers greater than 5 are the greater of the two.

Conclusion

In summary, although this paradox is incredibly surprising, it does not ultimately subvert our understanding of the wordl. It seems like we get information, out of nothing, but it turns out that the advantage gained is so small as to be negligible.

For further reading on this topic, you can consider looking at this Quanta article on the same topic.